3)a) 
1)область опред. x∈(-∞;5)∪(5;+∞)
2) нули: х= 0,125
3) решение неравенства: х∈(-∞;0,125]∪(5; +∞)
б) раскроем скобки: 2x²-6x+16-15x+3x²≥0
5x²-21x+16≥0
найдем нули: D=441-320=121, √121=11, x₁=3.2 x₂=1
решение неравенства: х∈(-∞;1]∪[3.2; +∞)
в) раскроем скобки: 2х²-5х+4-7х+3х²≤0
5х²-12х+4≤0
Найдем нули: D/4=36-20=16, √16=4
x₁=(6+4)/5=2, x₂=(6-4)/5=0.4
решение неравенства: [0.4;2]
г) раскроем скобки: 4х²-9х+30-8х<0<br> 4x²-17x+30<0<br>D=289-480<0, значит нулей нет, то при любом Х трехчлен принимает положительные значения, поэтому решений нет.<br>4) 
1) область определения: (-∞;-6)∪(-6;0)∪(0; +∞)
2) найдем нули: х²-2х-15=0
D/4=1+15=16, √16=4, x₁=1+4=5, x₂=1-4=-3
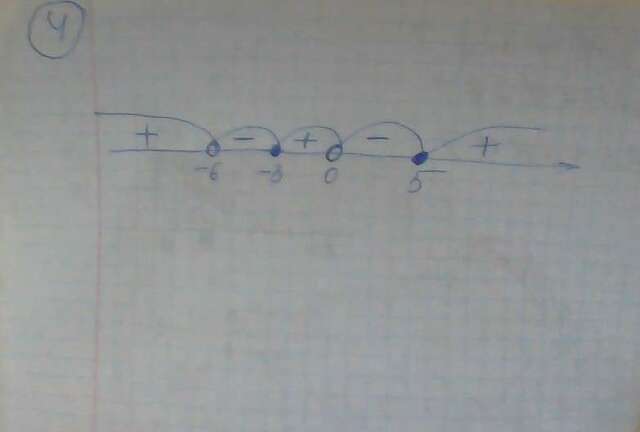
получили 5 интервалов и в каждом из них многочлен сохраняет знак постоянным: х∈(-∞; -6)∪(-3;0)∪(5; +∞) многочлен положителен, т.е. >0
х∈(-6; -3)∪(0; 5) многочлен принимает отрицательные значения, т.е. <0<br>рисунок на отдельном листе
ответ: (-6; -3)∪(0; 5)