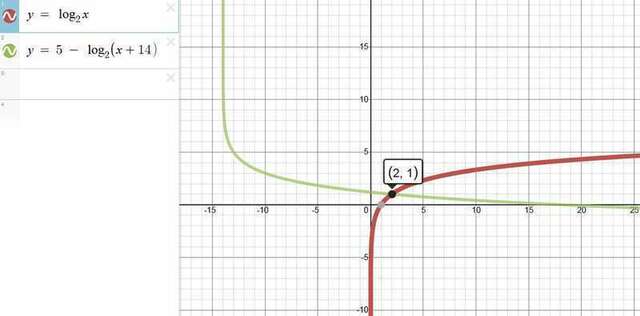
Если есть проблемы с отображением, смотрите снимок ответа, приложенный к нему.
====
Графики функций пересекаются. Чтобы найти пересечение, приравняем функции:

Вспоминаем свойство логарифмов:  и преобразуем выражение:
и преобразуем выражение:

Преобразуем выражение в экспоненциальную форму:

Итак, мы нашли координаты  (или по-другому абсциссы) точек пересечения графиков двух функций. Нас же просят найти ординаты, то есть координаты
(или по-другому абсциссы) точек пересечения графиков двух функций. Нас же просят найти ординаты, то есть координаты  точек пересечения этих графиков. Найти их просто: нужно подставить в одну из функций вместо
точек пересечения этих графиков. Найти их просто: нужно подставить в одну из функций вместо 
 , а затем
, а затем  :
:
 логарифма отрицательного числа не существует.
логарифма отрицательного числа не существует.

Итак, алгебра говорит, что на самом деле пересечение одно, и точка пересечения графиков имеет координаты  .
.
Проверим это графически. Смотрите рисунок, приложенный к ответу. Графически получается то же самое.
Итак, ордината или координата  точки пересечения двух графиков равна 1.
точки пересечения двух графиков равна 1.
Ответ: 1.