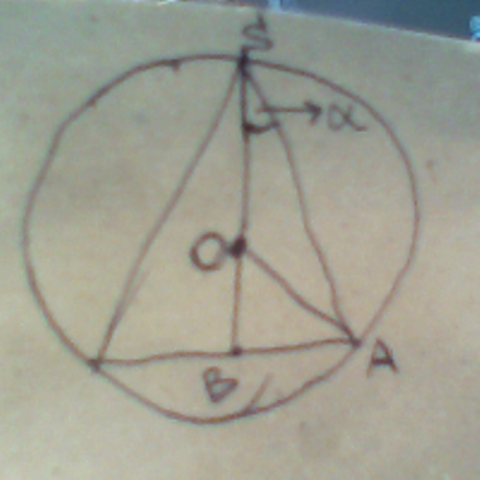
OS=OA=R=12
h=SB= ?
∡OSA=α
Vk=V = 1/3πr²h
r=h·tgα ⇒
V=1/3πh³·tg²α
h= OS+OB = R+OA·cos∡AOB=R+R·cos2α ⇒cos2α=(h-R)/R
r=Rsin2α ; OB=Rcos2α
Из тригонометрических формул ⇒
tg²α=(1-cos2α)/(1+cos2α) поставляя значение cos2α получим:
tg²α= (2R-h)/h ⇒⇒
V=1/3πh²·(2R-h)
Остался найти экстремумы h , при которых V ' = 0 ⇒⇒
[h²(2R-h)]' =0 ⇒⇒
4Rh - 3h²= 0
h= 4/3·R = 4/3 ·12 = 16