Точка движется вдоль оси х с постоянным ускорением а = –3 м/с^2, в начальный момент...

Question

Дан 1 ответ

Интереcующийся_zn · Answer 1 · 2018-04-25T15:02:03+0000

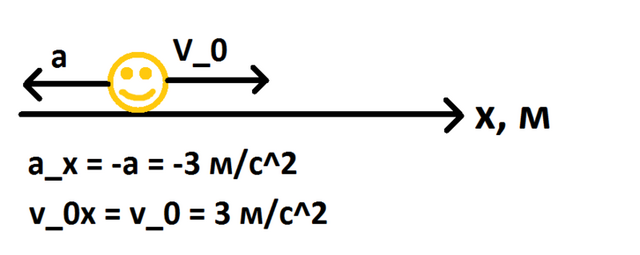
Если есть проблемы с отображением, смотрите снимок ответа, приложенный к нему.
====
Смотрите рисунок к задаче, приложенный к ответу.
Так как точка движется вдоль оси $x$ , то движение является прямолинейным, а поэтому все движение будем рассматривать только вдоль оси $x$ , и все характеристики движения (векторы скорости, ускорения) будем рассматривать в виде проекций на ось $x$ . Из условия имеем, что $a_x = -3 \frac{m}{s^2}, v_{0x} = 3\frac{m}{s}$ .
Так как векторы начальной скорости и ускорения тела противоположно направлены, то в определенный момент времени тело повернет и будет двигаться в противоположную сторону. Наша задача в таком случае найти путь, пройденный телом до поворота и после него. Для этого воспользуемся формулой $s_x = \frac{v_x^2 - v_{0x}^2}{2a_x}$ . В момент поворота тело имеет скорость $0 m/s$ (то есть $v_x = 0 \frac{m}{s}$ ), а начальная скорость и ускорение тела даны в условии. Воспользуемся данной формулой и найдем путь, пройденный телом до поворота:
$s_x=\frac{(0 \frac{m}{s})^2-(3 \frac{m}{s})^2}{2\cdot(-3 \frac{m}{s^2})} = \frac{-9 \frac{m^2}{s^2}}{-6 \frac{m}{s^2}} = 1.5 m$ . Отлично. Путь, пройденный телом до поворота, мы нашли. Теперь же для дальнейших расчетов нам понадобится узнать время, за которое тело прошло этот путь. Время узнаем из другой формулы:
$a_x = \frac{v_x - v_{0x}}{t} \\ t = \frac{v_x - v_{0x}}{ax}$
Как мы уже ранее выяснили, в момент, когда тело повернуло, его скорость была равна нулю, а начальная скорость и ускорение тела даны в условии задачи. Найдем время до поворота:
$t = \frac{0 \frac{m}{s} - 3 \frac{m}{s}}{-3 \frac{m}{s^2}} = \frac{-3}{-3} s = 1 s$ .
В условии задачи нас просят найти путь, пройденный телом за четыре секунды. До поворота в течение одной секунды тело прошло 1.5 метра. Нас интересует, какой путь прошло тело после поворота за $4 s - 1 s = 3 s$ . На этот раз путь будем искать по другой формуле, не зависящей от конечной скорости (нам она теперь неизвеста): $s_x = v_{0x}t + \frac{a_xt^2}{2}$
Теперь начальная скорость равна нулю, поскольку мы рассматриваем движение тела с момента его поворота. Найдем перемещение:
$s_x = 0 \frac{m}{s} \cdot 3 s - \frac{3 \frac{m}{s^2} \cdot (3s)^2}{2} = 0 m - 13.5 m = -13.5 m$
Ничего страшного, что перемещение отрицательно. Мы ищем путь, он неотрицателен, а так как движение прямолинейное, то путь найдем как модуль перемещения:
$|s_x| = 13.5m$
========
Итак, мы нашли путь до поворота и после поворота, осталось только сложить их и получить общий путь за 4 секунды:
$1.5 m + 13.5 m = 15 m$
Это ответ.