Окружность с центром О и радиусом 16см описана около ΔАВС так, что ∠ОАВ-30°, ∠ОСВ=45°....

Question

Окружность с центром О и радиусом 16см описана около ΔАВС так, что ∠ОАВ-30°, ∠ОСВ=45°. Найдите стороны треугольника

Answer 1

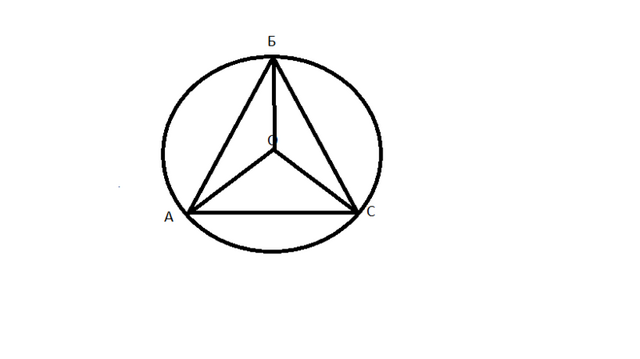
Рассмотрим ΔАОВ
Он равнобедренный(т.к.АО=ОВ=радиусу)
Значит, уг ОАВ=ОВА=30
Угол АОВ=180-(2*30)=120косинус 120гр=косинусу180-120=60 гр(формулы приведения)
По теореме косинусов АВ^2=AO^2+ВО^2-2*AO*ВО*cos60
АВ^2=16*16+16*16-2*16*16*0.5=256+256-256=256
АВ=16
Рассмотрим ΔВОС , Он равнобедренный (т.к. ВО=ОС=радиусу)
угол ОСВ=СВО=45
Отсюда, угол ВОС=180-(45+45)=90
По теореме Пифагора ВС^2=OC^2+ОВ^2=16*16+16*16=512
ВС=16 корней из 2х  
Ответ: АВ=16, ВС=16 корней из 2х

---