1) Найти область определения функции: x ≠ 0.
2) Найти точки пересечения координат: так как х находится в знаменателе дроби, то пересечения с осью у нет.
Для определения пересечения с осью х надо решить уравнение 2х²+(4/х) = 0.
Приведём к общему знаменателю: (2х³+4)/х = 0.
Дробь равна 0, когда числитель равен 0:
2х³+4=0,
х³=-4/2 = -2,
х =∛(-2) =
-1.25992.
3) Найти промежутки возрастания и убывания:
Находим производную: y' = 4x-(4/x²) и приравниваем её 0:
4x-(4/x²) = 0.
Приведём к общему знаменателю: (4х³-4)/х² = 0.
Дробь равна 0, когда числитель равен 0:
4х³-4 = 0,
х³ = 4/4 = 1,
х= ∛1 = 1.
Если производная отрицательна, то функция убывает, если производная положительна, то функция возрастает.
Находим значения производной вблизи критической точки:
х -2
-1 0
0.5
1 2
y ' -9 -8
- -14
0 7.
Отсюда видно:
Функция возрастает x > 1 или х ∈ (1;∞)
,
убывает х < 0; 0 ∈ (-∞;0) ∪ (0;1].
4) Найти точки экстремума:
Она уже найдена - это локальный минимум в точке х = 1.
Вблизи этой точки производная функции меняет знак с минуса на плюс.
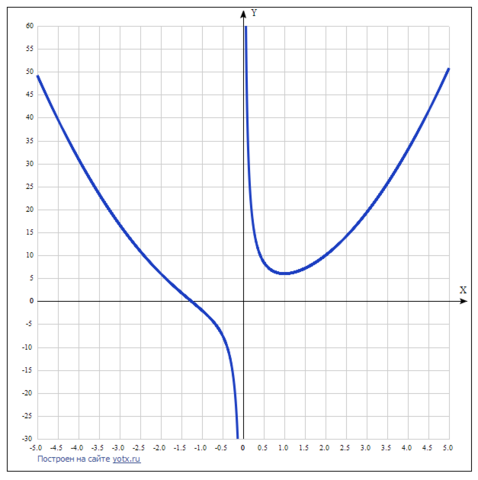
5) Построить график - он дан в приложении.