В равнобедренном треугольнике основание равно 10 см, а боковая сторона равна 13 см.
Найти радиус окружности, вписанной в этот треугольник.
--------
Формула радиуса вписанной в треугольник окружности:
r=S/p,
где -S- площадь треугольника, р - его полупериметр,
S=a•h:2.h- высота треугольника, а - сторона, к которой она проведена.
Высота равнобедренного треугольника, опущенная на основание - еще медиана и биссектриса.
Она делит треугольник на два равных прямоугольных, в которых гипотенуза - боковая сторона, а катетами являются высота h и половина основания.
По т.Пифагора
h=√(13²-5²)=
12 cм
S=12•10:2=
60 cм²
р=Р:2=(13+13+10):2=
18 см
r=60
:18=10
:3=
3¹/₃ см
------
Радиус вписанной в равнобедренный треугольник окружности можно найти из подобия треугольников, на которые радиус, проведенный в точку касания, делит половину исходного, т.е. прямоугольный треугольник.
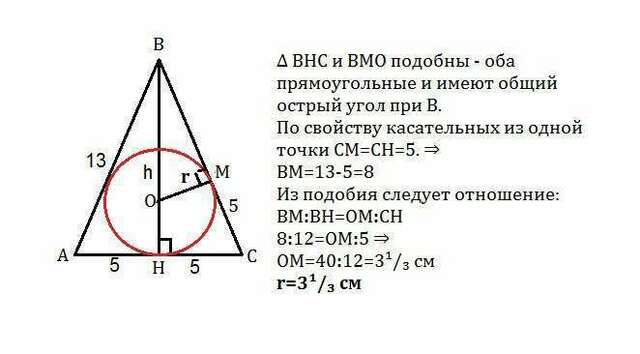
Пусть дан треугольник АВС, ВН его высота.
Высоту найдем как описано выше.
Проведем
радиус ОМ в точку касания на ВС.
∆ ВНС и ВМО подобны - оба прямоугольные и имеют общий острый угол при В.
По свойству касательных из одной точки СМ=СН=5. ⇒
ВМ=13-5=8
Из подобия следует отношение:
ВМ:ВН=ОМ:СН
8
:12=ОМ
:5 ⇒
ОМ=40:
12=
3¹/₃ см
r=
3¹/₃ см