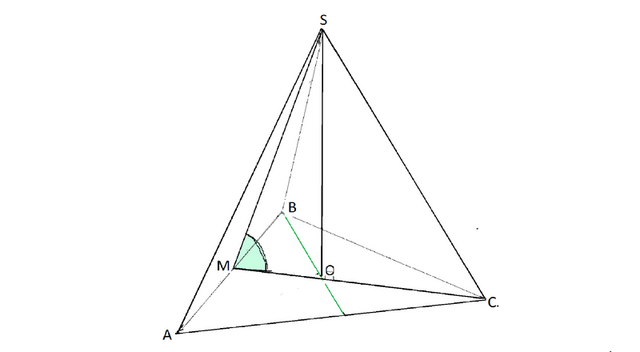
Для того, чтобы ответить на вопрос задания, нужно определиться, что ищем тангенс угла, образованного апофемой SM и высотой MC основания ABC.
Bспомним, что основание высоты правильной пирамиды находится в точке пересечения высот основания, а сама высота перпендикулярна основанию.
Эта точки делит их ( потому что высоты правильного треугольника и медианы и биссектрисы) в отношении 2:1, считая от вершины.
Следовательно, основание О высоты SO пирамиды отстоит от боковой грани на
одну треть высоты MC плоскости правильного треугольника.
Это расстояние 6:3=2
Так как высота пирамиды SO, треть MO высоты основания и апофема SM являются сторонами прямоугольного трегольника SOM,
тангенс угла SMO
между плоскостью боковой грнани и плоскости основания находим отношением противолежащего углу катета к прилежащему.
tg SMO= SO:OM=16:2= 8