Длина основание треугольника равна 14, а медианы, проведённые к боковым сторонам, равны 3√7 и 6√7. Найдите длины боковых сторон этого треугольника
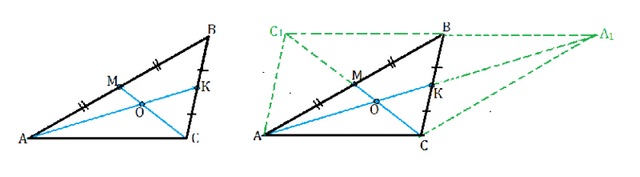
Пусть дан ∆ АВС, медианы АК и СМ, точка их пересечения - О.
Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины.
Тогда СО=2/3·СМ=2√7,
AO=2/3·АК=4√7,
ОК=1/3·АК=2√7
По т.косинусов
АС²=АО²+СО²-2*АО*СО*cos ∠АОС
cos ∠АОС=(АС²-АО²+СО²):(-2*АО*СО)
cos ∠АОС=[14²-(4√7)²-(2√7)²]:[-2*(4√7)*(2√7]
cos ∠АОС= -56:2*56= -1/2 - это косинус 120º
Рассмотрим ∆ КОС.
ОК=OC=2√7 (см. выше)
⇒ КОС- равнобедренный.
∠ КОС =∠КОА-∠АОС=180º-120º=60º ⇒ ∆ СОК - правильный,
КС=2√7
BC=2KC=4√7
Из ∆ АМО
АМ²=МО+АО-2*МО*АО*cos∠АОМ
АМ²=(√7)²+(4√7)²-2*(√7)*(4√7)*1/2*cos∠АОМ
АМ²=7+16*7-2*4*7*1/2
АМ²=7+16*7-4*7=7(1+16-4)=91
АМ=√91
AB=2√91
----------
Можно продлить медианы на их длину ( см. рис) и достроить треугольник до параллелограммов АВА₁С и АСВС₁
По свойству диагоналей параллелограмма
АА₁²+ВС²=2(АВ²+АС²)
и
СС₁²+АВ²=2(АС²+ВС²)
Пусть АВ=с, ВС=а
Тогда можно составить систему уравнений:
|(2*6√7)²+a²=2(c²+14²)
|(2*3√7)²+c²=2(14²+a²)
Решив систему, получим АВ=2√91, BC=4√7