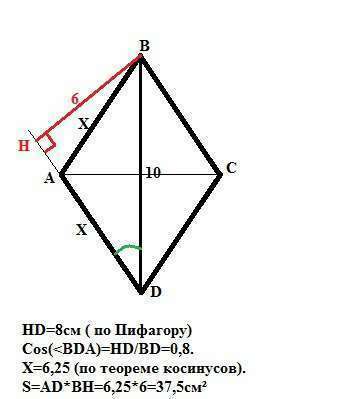
Дан ромб АВСD с диагональю ВD и высотой BH.
В прямоугольном треугольнике ВНD по Пифагору найдем катет HD:
HD=√(ВD²-ВН²)=√(100-36)=8см. Тогда Cos(В треугольнике АВD по теореме косинусов имеем:
АВ²=АD²+BD²-2*AD*BD*Cos(Х²=Х²+100-2Х*10*0,8. Отсюда Х=100/16=6,25см. Это сторона ромба.
Тогда его площадь равна произведению стороны на высоту ромба.
S=6*6,25=37,5см².