Дан квадрат со стороной а=6 см, S=6^2=36 см^2
Проведем ось симметрии по диагонали квадрата, разрежем и получим 2 конгруэнтных равнобедренных прямоугольных треугольника.
Из данных треугольников имеющих катеты а = сторонам а квадрата, и гипотенузу = диагонали квадрата=√2S=6√2 см.
Сложим из данных треугольников один равнобедренный прямоугольный треугольник:
- в основании - удвоенная сторона квадрата: 2а=2*6=12 см:
- катеты = dΔ=6√2 (проверить это можно, используя формулу Пифагора для каждого из 2-х прямоугольных треугольников, получившихся при разрезании квадрата по диагональной оси симметрии: c^2=6^2+6^2 => c=√72=6√2 см;
- SΔ=1/2b*h=1/2*12*6=36 см^2 = S квадрата
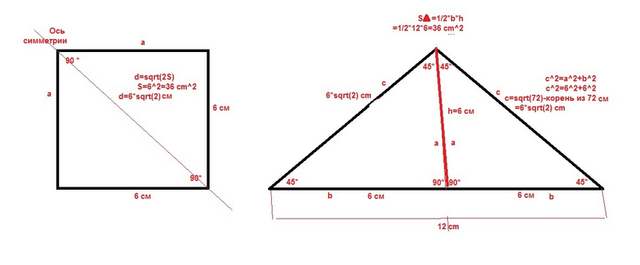
Чертеж с расчетами во вложении