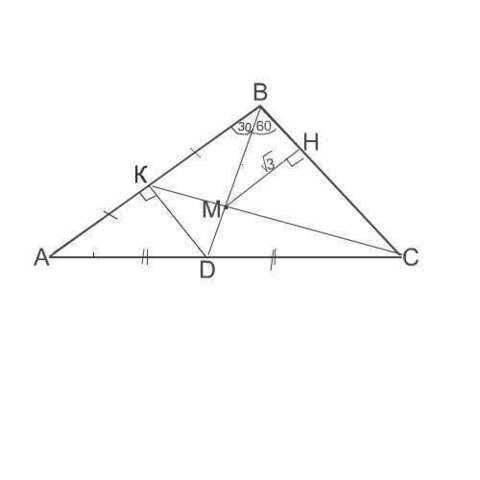
В треугольнике АВС медиана ВD составляет со стороной ВС угол DВС = 60º.
Точка пересечения медиан удалена от прямой ВС на корень из 3 см
а)найдите В
б)Найдите АВ,если угол АВD=30º
-------------
Решение.
Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины угла.
Следовательно, ВD=ВМ:2·3
Кратчайшее расстояние от точки до прямой - перпендикуляр. МН ⊥ВС
ВМ найдем из треугольника ВМН.
ВМ=МН:sin (60º)=(√3:√3)·2=2см
ВD=2:2·3=3cм
Так как по условию ∠АВD=30º,
то ∠АВС=30º+60º=90º.
Следовательно, треугольник АВС прямоугольный.
АС в нем - гипотенуза.
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна её половине. И, наоборот, половина гипотенузы равна медиане.
АD=ВD=3 cм
Треугольник АВD равнобедренный.
Проведем в нем высоту DК, которая является и медианой, и биссектрисой по свойству высоты равнобедренного треугольника.
Поэтому ∠КDА=60º
АК:АD=sin(60º)
АК=АD·sin(60º)
АК=3·√3):2=1,5√3
АВ=2 АК=3√3