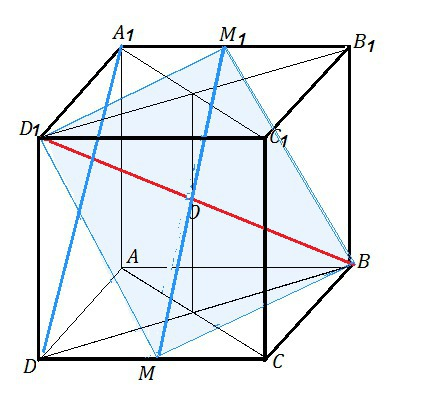
Дан куб с ребром равный 1. Найти угол между прямыми DA1 и BD1
ВD1 - диагональ куба. DА1 - диагональ его грани.
Проведем через середину диагонали куба прямую, параллельную DА1 и пересекающую ребра А1В1 и DС. Оба отрезка пересекутся в центре куба О и делятся им пополам.
Стороны четырехугольника МD1М1В равны, т.к. являются гипотенузами треугольников с равными катетами, следовательно, этот четырехугольник - ромб, и его диагонали М1М и ВD1 пересекаются под углом 90º
Найти угол между МО и ВО можно и из ∆ ВОМ по т.косинусов.
ВМ²=МО²+ВО² - 2МО•BO•cos∠BOM
cos∠BOM=(ВМ²-МО²+ВО²):(- 2МО•BO)
МО=половине диагонали грани,
ВО - половине диагонали куба.
Вычислить длины сторон ∆МОВ не составит труда. Результат решения уравнения - косинус угла ВОМ=0, и это косинус 90º