Правильная призма — это прямая призма, основанием которой является правильный многоугольник, в случае правильной четырехугольной призмы - основанием призмы является квадрат.
Правильная четырехугольная призма - прямоугольный параллелепипед.
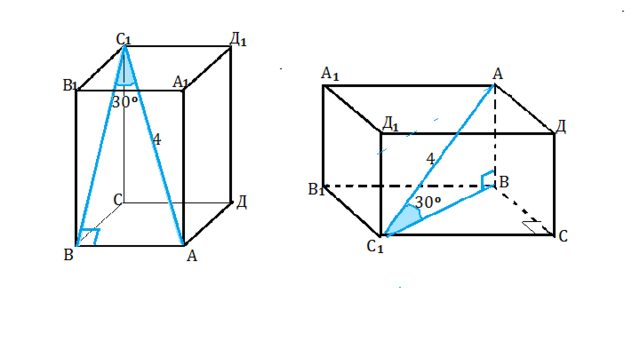
Пусть данная призма - АВСДА₁В₁С₁Д₁
Сделаем рисунок. (
Во втором рисунке призма «уложена" на боковую грань для большей наглядности. )
Решение.
АВ ⊥ ВС1 (если прямая перпендикуляра плоскости, она перпендикулярна любой прямой на этой плоскости).
Диагональ АС₁ -
гипотенуза прямоугольного треугольника АВС₁
Тогда АВ, сторона основания, противолежащая углу 30º, равна половине АС₁
АВ=ВС=СД=ДА=2
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
D²=а²+b²+c²16=2²+2²+h²⇒
h²=16-8=8
h=√8=2√2
Площадь боковой поверхности призмы равна произведению периметра ее основания на высоту.
Р=4*2=8 см
Ѕ бок=8*2√2=16√2 см²
-------------.
Высоту призмы можно найти иначе.
а) Сначала найдем диагональ ВС₁ боковой грани- она равна АС₁·cos 30°=(4 √3):2=2 √3
Высоту h трапеции найдем по т. Пифагора из треугольника ВСС₁
h² =(2 √3)²+2²=12-4=8
h=2√2
-------
б) Тот же результат получим, найдя по т. Пифагора из треугольника АВС
₁ диагональ ВС
₁ боковой грани, затем из прямоугольного треугольника ВСС₁
высоту призмы СС₁.