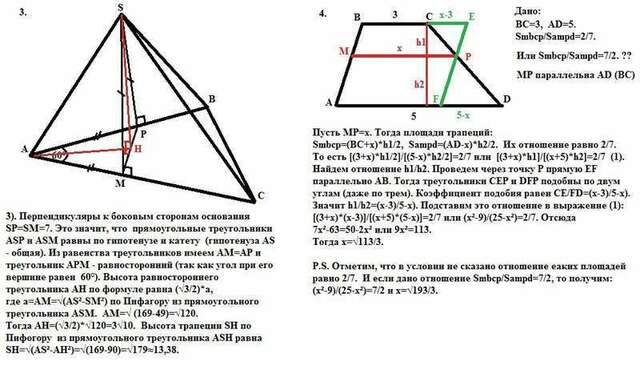
3). Перпендикуляры к боковым сторонам основания SP=SM=7. Это значит, что прямоугольные треугольники АSР и АSМ равны по гипотенузе и катету (гипотенуза АS - общая). Из равенства треугольников имеем АМ=АР и треугольник АРМ - равносторонний (так как угол при его вершине равен 60°). Высота равностороннего треугольника АН по формуле равна (√3/2)*а, где а=АМ=√(АS²-SМ²) по Пифагору из прямоугольного треугольника АSМ.
АМ=√(169-49)=√120.Тогда АН=(√3/2)*√120=3√10.
Высота трапеции SН по Пифогору из прямоугольного треугольника АSН равна
SН=√(АS²-АН²)=√(169-90)=√179≈13,38.
4. Пусть МР=х. Тогда площади трапеций:
Smbcp=(BC+x)*h1/2, Sampd=(АD-x)*h2/2. Их отношение равно 2/7.
То есть [(3+x)*h1/2]/[(5-x)*h2/2]=2/7 или [(3+x)*h1]/[(x+5)*h2]=2/7 (1).
Найдем отношение h1/h2. Проведем через точку Р прямую EF параллельно АВ. Тогда треугольники СЕР и DFP подобны по двум углам (даже по трем). Коэффициент подобия равен СЕ/FD=(х-3)/5-х). Значит h1/h2=(х-3)/5-х).
Подставим это отношение в выражение (1):
[(3+x)*(х-3)]/[(x+5)*(5-х)]=2/7 или (х²-9)/(25-х²)=2/7. Отсюда
7х²-63=50-2х² или 9х²=113.
Тогда х=√113/3.
P.S. Отметим, что в условии не сказано отношение каких площадей равно 2/7. И если дано отношение Smbcp/Sampd=7/2, то получим:
(х²-9)/(25-х²)=7/2 и х=√193/3.
5) . Теорема: "Если из точки, лежащей вне окружности, проведены две
секущие, то произведение одной секущей на её внешнюю часть равно
произведению другой секущей на её внешнюю часть". Пусть внешняя часть второй секущей равна х, тогда согласно этой теореме:
(47+9)*9=(72+2х)*х. Отсюда 72х²+2х-504=0 или х²+36х-252=0.
Решаем квадратное уравнение и получаем х=-18+24=6. Отрицательный корень нас не удовлетворяет. Тогда длина второй секущей равна (72+6)+6=84.
Ответ: длина второй секущей равна 84.