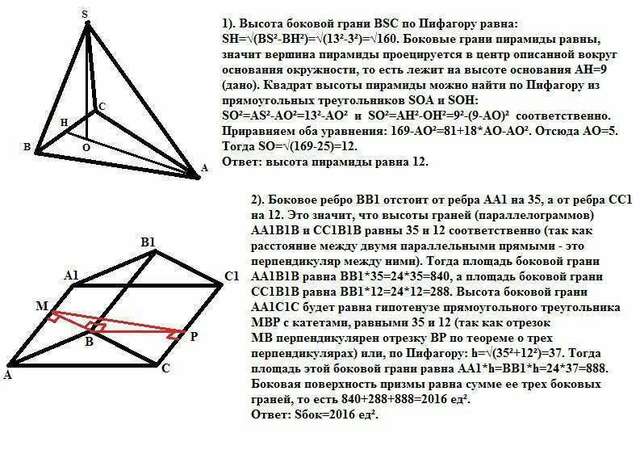
1). Высота боковой грани ВSС по Пифагору равна:
SH=√(ВS²-ВН²)=√(13²-3²)=√160. Боковые грани пирамиды равны, значит вершина пирамиды проецируется в центр описанной вокруг основания окружности, то есть лежит на высоте основания АН=9 (дано). Квадрат высоты пирамиды можно найти по Пифагору из прямоугольных треугольников SОА и SОН:SО²=АS²-АО²=13²-АО² и SО²=АН²-ОН²=9²-(9-АО)² соответственно.Приравняем оба уравнения: 169-АО²=81+18*АО-АО². Отсюда АО=5. Тогда SО=√(169-25)=12.Ответ: высота пирамиды равна 12. 2). Боковое ребро ВВ1 отстоит от ребра АА1 на 35, а от ребра СС1 на 12. Это значит, что высоты граней (параллелограммов) АА1В1В и СС1В1В равны 35 и 12 соответственно (так как расстояние между двумя параллельными прямыми - это перпендикуляр между ними). Тогда площадь боковой грани АА1В1В равна ВВ1*35=24*35=840, а площадь боковой грани СС1В1В равна ВВ1*12=24*12=288. Высота боковой грани АА1С1С будет равна гипотенузе прямоугольного треугольника МВР с катетами, равными 35 и 12 (так как отрезок МВ перпендикулярен отрезку ВР по теореме о трех перпендикулярах) или, по Пифагору: h=√(35²+12²)=37. Тогда площадь этой боковой грани равна АА1*h=ВВ1*h=24*37=888. Боковая поверхность призмы равна сумме ее трех боковых граней, то есть 840+288+888=2016 ед².Ответ: Sбок=2016 ед².