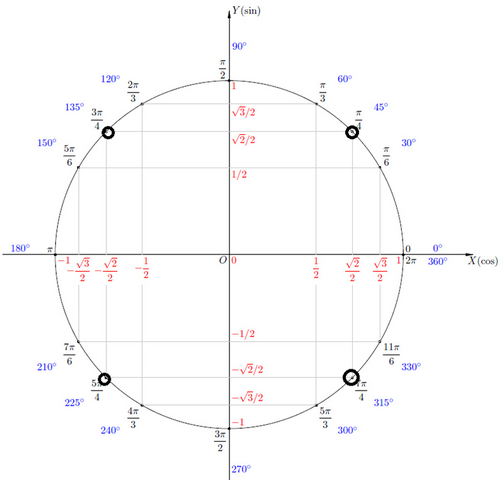
Сначала упростим. Как видно из тригонометрического круга, который я приложила к ответу, 7π/2 - это 3π+π/2 или 2π+π+π/2
2π-совпадает с углом "0", поэтому его смело можно им заменить, т.е.:
2π+π+π/2=0+π+π/2=π+π/2.
Получаем выражение:
20cos(7π/2+a)=20cos(π+π/2+a)=20cos(π+(π/2+a)).
Примечание:
Если мы к углам пи или 2пи прибавляем (или отнимаем) какой-то угол, то тригонометрическая функция не меняется (косинус остаётся косинусом, а синус-синусом), а если мы прибавляем (или отнимаем) какой-то угол от углов пи/2 или 3пи/2, то косинус меняется на синус, к примеру:cos(пи/2 + 30°)=косинус во второй четверти меньше нуля-ставим минус и угол пи/2 - поэтому косинус меняем на синус= -sin30°.
В нашем случае прибавляемый угол = π/2+a
Воспользуемся вышеописанными правилами:
20cos(π+(π/2+a))
Как видно из тригонометрического круга, если к пи прибавлять какой-либо угол, то он будет находиться в 3 четверти, где косинус отрицательный, поэтому ставим минус перед нашим выражением. Из примечания также следует:
20cos(π+(π/2+a)) = -20cos(π/2+a)
Теперь разложим косинус как косинус суммы:
cos(x+y)=cosx*cosy-sinx*siny
Применим данную формулу для нашего случая:
-20cos(π/2+a)=-20*(сosπ/2*cosa-sinπ/2*sina)
Опять же из тригонометрического гура видно, что косинус π/2 = 0, поэтому первое слагаемое превращается в ноль, а sinπ/2=1. В связи с этим запишем:
-20*(сosπ/2*cosa-sinπ/2*sina)=-20(0-1*sina)=-20*(-sina)=20sina.
Мы знаем, что cosa=-7/25. Из тригонометрической единицы
(cos²а+sin²а=1) Найдём sina:sin²а=1-cos²а=1-(-7/25)²=1-49/625=625/625 - 49/625 = (625-49)*625=576/625
значит sina=√(576/625)=24/25.
В итоге получим:
20sina=20*24/25=4*24/5=19,2-это и будет ответ.