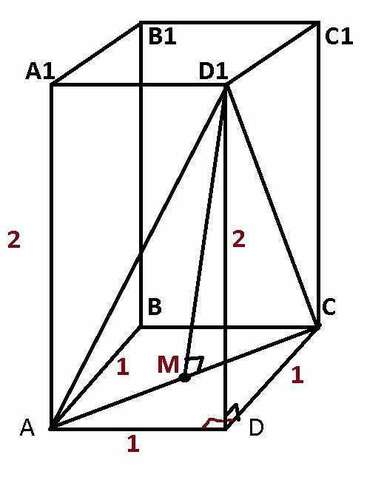
Т.к. противолежащие ребра равны, получается AB=CD=1, AA1=DD1=2. По теореме Пифагора: AD1=√(1²+2²)=√5. Аналогично СD1=√5. AC=√(1²+1²)=√2. Рассмотрим ΔACD1: Он равнобедренный, т.к. AD1=CD1=√5. Соответственно , высота этого треугольника (назовем её D1M), проведенная к основанию АС и будет являться искомым расстоянием от точки D1. В равнобедренном треугольнике высота, проведенная к основанию, является и медианой, поэтому AM=CM=(√2)/2. Теперь по т. Пифагора можно найти катет D1M ΔD1MA: D1M=√(AD1²-AM²)=√((√5)²-((√2)/2)²)=√(5-1/2)=√4.5