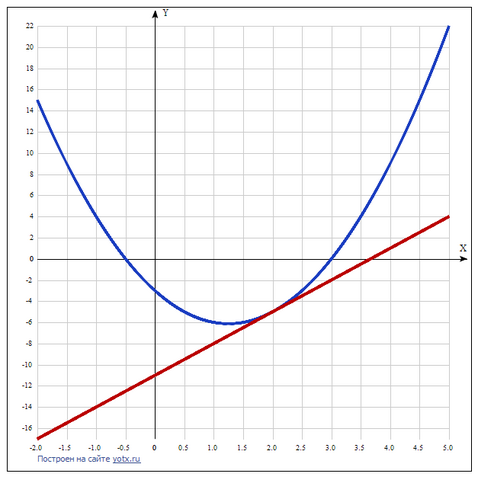
F(x)=y=2x²-5x-3, xо=2.
Уравнение касательной имеет вид:
fк = f(xo) + f '(xo)*(x-xo).
Находим производную:
f '(x) = 4х - 5.
Значение производной в точке хо:
f '(xо) = 4*2 - 5 = 8 - 5 = 3.
Значение функции в точке хо:
f(xo) = 2*2² - 5*2 - 3 = 8 - 10- 3 = -5.
Тогда fк = -5 + 3(х - 2) = -5 + 3х - 6 = 3х - 11.