8.2.
К. в.
1) 3 прямые
2) бесконечное число прямых
3) одну прямую
З.
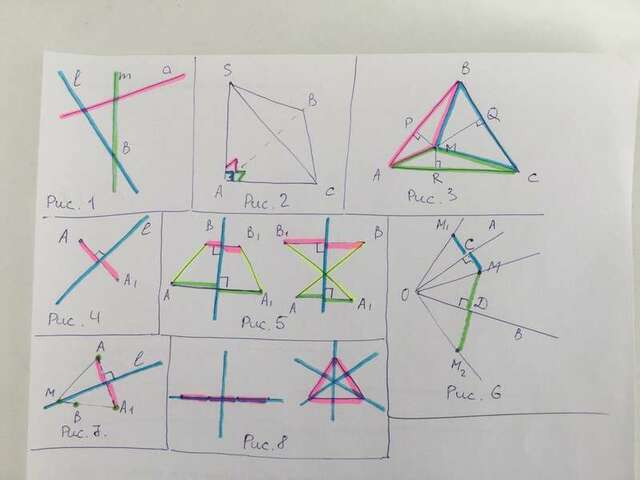
1) Из прямых l и m лишь одна может быть перпендикулярна прямой a (см. рис. 1).
2) Одна из вершин треугольной пирамиды может быть образована рёбрами, лежащими на трёх взаимно перпендикулярных прямых (см. рис. 2).
3) (См. рис. 3.) У равностороннего треугольника все стороны равны (обозначим их a), все высоты тоже равны (обозначим их h).
S ΔABC = 1/2·a·h
С другой стороны, S ΔABC = S ΔAMB + S ΔBMC + S ΔAMC.
Т. е.: 1/2·a·h = 1/2·a·MP + 1/2·a·MQ + 1/2·a·MR.
Откуда: h = MP + MQ + MR.
8.3
К.в.
1) а) луч имеет одну ось симметрии -- прямую, на которой он лежит; б) осями симметрии отрезка являются прямая, содержащая сам отрезок (она одна), а также прямые, содержащие срединные перпендикуляры к этому отрезку (на плоскости она одна, а в пространстве их бесконечное число); в) прямая содержит бесконечное число осей симметрии (саму прямую и любой перпендикуляр к ней); д) плоскость содержит бесконечное число осей симметрии.
2) Существует много определений. Лучше посмотреть в изучаемом параграфе :)
З.
1) и 2) Ось симметрии должна содержать срединный перпендикуляр отрезка АА₁. (см. рис. 4).
3) (См. рис. 5). Ось симметрии обязательно будет содержать срединный перпендикуляр отрезков АА₁ и ВВ₁.
4) Из равенств ΔОCМ = ΔОCМ₁ и ΔОDМ = ΔОDМ₂ следует равенство углов: 5) (Cм. рис. 7) Строим точку A₁, симметричную точке А относительно прямой l. Через точки А₁ и В проводим прямую А₁В. М -- точка пересечения прямых А₁В и l. Прямая l будет биссектрисой Задача во второй части вопроса может не иметь решения, если точки А и В симметричны относительно прямой l. Тогда точка В₁ совпадёт с А и прямая АВ₁ вырождается в точку.
6) 2 или 3 оси симметрии (см. рис. 8).
7) Куб имеет один центр симметрии - в точке пересечения диагоналей куба, и 9 осей симметрии -- прямые, содержащие диагонали куба, перпендикуляры к граням куба и срединные перпендикуляры к параллельным рёбрам куба, не принадлежащим одной грани.