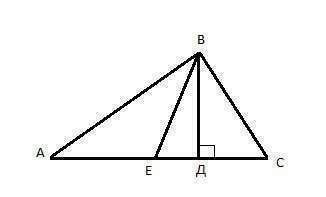
Построим треугольник АВС (Сторона АС=8 см.) Проведем к
стороне АС высоту ВД (4 см) и медиану ВЕ (5 см). см. приложение.
1. Рассмотрим треугольник ВДЕ: угол ВДЕ=90 градусов. Катет
ВД=4 см. Гипотенуза ВЕ=5 см
По теореме Пифагора найдем ДЕ:
ДЕ=√(ВЕ^2-ВД^2)= √(5^2-4^2)= √(25-16)= √9=3 см.
Так как ВЕ – медиана АЕ=СЕ=8/2=4 см.
Зная это найдем СД и АД:
СД=СЕ-ДЕ=4-3=1 см.
АД=АЕ+ДЕ=4+3=7 см.
2. Найдем сторону АВ.
Рассмотрим треугольник АВД – угол АДВ= 90 градусов. Катет
АД=7см. Катет ВД=4 см.
По теореме Пифагора найдем АВ:
АВ=√(АД^2+ВД^2)= √(7^2+4^2)= √(49+16)= √65 см
(приблизительно 8,06 см)
3. Найдем сторону ВС.
Рассмотрим треугольник ВСД – угол ВДС= 90 градусов. Катет СД=1см.
Катет ВД=4 см.
По теореме Пифагора найдем АВ:
ВС=√(СД^2+ВД^2)= √(1^2+4^2)= √(1+16)= √15 см (приблизительно
3,87 см)
Ответ: АВ= √65 см. ВС= √15 см