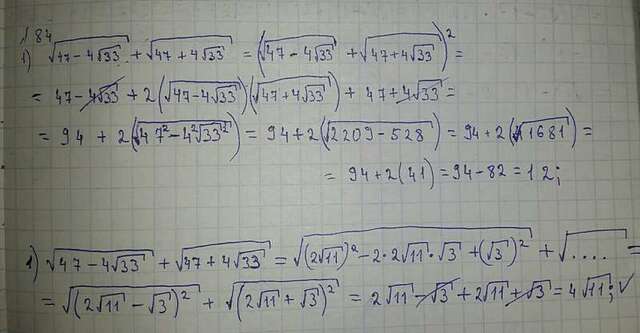Вычислите:

Решил выделением квадрата в подкоренном выражении, и получил правильный ответ, который равен  .
.
А решая возведением в квадрат всего выражения получил в ответе 12. Разве так нельзя? Добавил снимок решений первым и вторым способом.
Другой пример:
![\sqrt[3]{5\sqrt2-7}*\sqrt{3+2\sqrt2} \sqrt[3]{5\sqrt2-7}*\sqrt{3+2\sqrt2}](https://tex.z-dn.net/?f=%5Csqrt%5B3%5D%7B5%5Csqrt2-7%7D%2A%5Csqrt%7B3%2B2%5Csqrt2%7D)
Выделил квадрат под корнем второго множителя, и это же выражение оказалось под корнем первого множителя, но в кубе. Т.е. вот:
![\sqrt{3+2\sqrt2}=\sqrt{(\sqrt2)^2+2\sqrt2+1}=\sqrt{(\sqrt2+1)^2}=\sqrt2+1;\\\sqrt[3]{(\sqrt2-1)^3}=\sqrt[3]{(\sqrt2)^3-3(\sqrt2)^2+3\sqrt2-1}=\sqrt[3]{5\sqrt2-7};\\ \sqrt[3]{5\sqrt2-7}*\sqrt{3+2\sqrt2}=(\sqrt2-1)(\sqrt2+1)=2-1=1 \sqrt{3+2\sqrt2}=\sqrt{(\sqrt2)^2+2\sqrt2+1}=\sqrt{(\sqrt2+1)^2}=\sqrt2+1;\\\sqrt[3]{(\sqrt2-1)^3}=\sqrt[3]{(\sqrt2)^3-3(\sqrt2)^2+3\sqrt2-1}=\sqrt[3]{5\sqrt2-7};\\ \sqrt[3]{5\sqrt2-7}*\sqrt{3+2\sqrt2}=(\sqrt2-1)(\sqrt2+1)=2-1=1](https://tex.z-dn.net/?f=%5Csqrt%7B3%2B2%5Csqrt2%7D%3D%5Csqrt%7B%28%5Csqrt2%29%5E2%2B2%5Csqrt2%2B1%7D%3D%5Csqrt%7B%28%5Csqrt2%2B1%29%5E2%7D%3D%5Csqrt2%2B1%3B%5C%5C%5Csqrt%5B3%5D%7B%28%5Csqrt2-1%29%5E3%7D%3D%5Csqrt%5B3%5D%7B%28%5Csqrt2%29%5E3-3%28%5Csqrt2%29%5E2%2B3%5Csqrt2-1%7D%3D%5Csqrt%5B3%5D%7B5%5Csqrt2-7%7D%3B%5C%5C++%5Csqrt%5B3%5D%7B5%5Csqrt2-7%7D%2A%5Csqrt%7B3%2B2%5Csqrt2%7D%3D%28%5Csqrt2-1%29%28%5Csqrt2%2B1%29%3D2-1%3D1)
Скорее мне больше повезло с этим примером, т.к. второй множитель помог. А вообще есть ли лучший способ выделить квадрат или куб, т.е. как их "увидеть"? ...даже не знаю как правильнее изложить свой вопрос, надеюсь поймете.
Прошу модераторов НЕ удалять сразу. Я возможно получу объяснения/ответы в личные сообщения, тогда и напишу вам, что можете удалить, в случае чего.