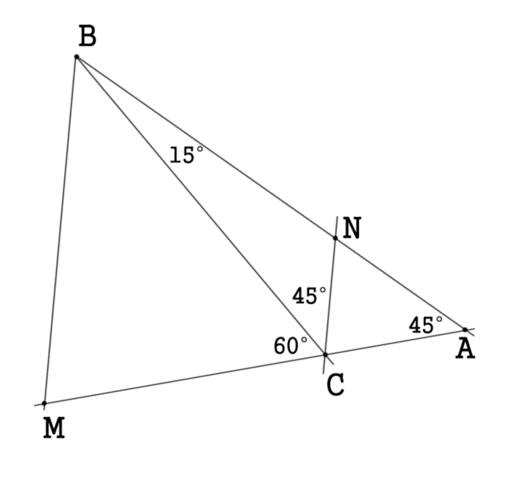
Исходя из того, что в любом треугольнике сумма углов равна

легко понять, что

Для любого треугольника верно, что отношение любой его стороны к синусу противолежащего угла – постоянно, тогда:
[1]

Проведём

так, чтобы

Тогда

Опять же из соотношения синусов:
[2]

Перемножим выражения [1] и [2]:


[3]

Учитывая, что:

и

а значит:

и

получим из выражения [3] :



Это как раз и позволит разрешить поставленный вопрос.

т.е.: NA : NB = 1 : 2 = CA : CM .
По Теореме Фалеса, пропорциональные отрезки на сторонах треугольника отсекаются параллельными прямыми, а значит:


О т в е т :