Задание **...

Question

Дано ответов: 2

Правильный ответ

Я решил тоже поучаствовать, хотя предыдущее решение дает верный ответ. Все обозначения у меня на рисунке, O1D II EK (то есть O1EKD - прямоугольник).
Легко вычислить по теореме Пифагора (O1O2 = √(2R^2 + 2r^2); O2D = R - r), что O1D = EK = R + r; (ну, r - радиус меньшей окружности, R - большей).
Осталось заметить, что угол, который надо найти ∠EMP1 = ∠P2O2K; - у них стороны перпендикулярны.
(Примечание. Поскольку уравнения "не знают", для какого угла их составляют, по идее должно получиться уравнение, которое даст сразу оба ответа)
Если обозначить искомый угол ∠EMP1 = γ; то ∠EMO1 = ∠MO2K = γ/2;
Очевидные соотношения MK = R*tg(γ/2); EM*tg(γ/2) = r; MK + EM = EK = R + r; дают уравнение для t = tg(γ/2);
(R + r)*t - R*t^2 = r; или t^2 - t*(R + r)/R + r/R = 0;
Решение этого квадратного уравнения можно представить в виде
t = (R + r)/(2R) +- (R - r)/(2R); или t1 = 1; t2 = r/R;
Первый случай соответствует углу γ = 90°; второй можно записать в виде γ = 2*arctg(r/R); это по сути тот же ответ, что и в другом решении.

Я взялся за это, чтобы понять, почему при таком расстоянии между центрами получается прямой угол. По сути тут задача о расстоянии между центрами вписанной и вневписанной окружностей для треугольника. Поэтому это и было интересно. Связь я увидел уже после того, как набрал решение. И это все упростило до предела. Вот во что превращается решение.
Получается, что ПРОЕКЦИЯ O1O2 на EK равна сумме радиусов. Но это сразу означает, что внутренняя касательная ПРОЕКТИРУЕТСЯ на внешнюю касательную в точку. То есть перпендикулярна ей. Конечно, речь идет об одной из ДВУХ внутренних касательных, к примеру, NM проектируется на нижнюю внешнюю касательную в точку N, а вторая внутренняя касательная, симметричная NM относительно O1O2, проектируется на EM в точку, симметричную N.
Это, по сути, все решение, потому что сразу MK = NP1 = r; (тут разберитесь, MK = NP1, всегда, то есть - в произвольном случае двух не пересекающихся окружностей, а почему?) => EM = R; tg(∠EMO1) = r/R; это всё!

cos20093_zn (69.9k баллов) 22 Апр, 18

gartenzie_zn · Answer 1 · 2018-04-22T06:55:49+0000

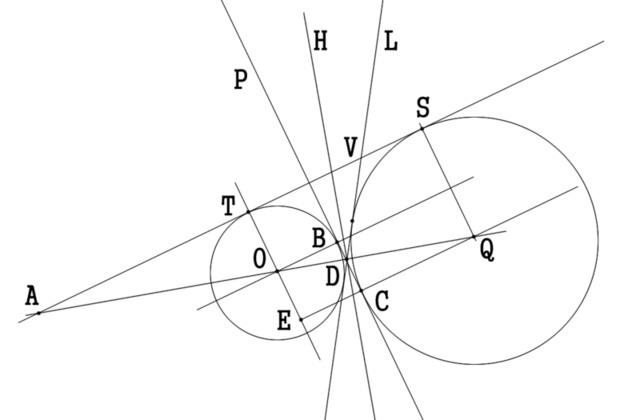
Вообще говоря, внутренних касательных две, а поэтому значений искомого угла будет два. Один из этих углов будет прямым, а для второго можно найти лишь параметрическое выражение синуса или косинуса.

Покажем это.

Сначала сделаем построение по условию задачи и введём соответствующие обозначения.

Центр малой окружности   $O \ ,$    и соответственно   $OB = r \ .$

Центр большой окружности   $Q \ ,$    и соответственно   $QC = R \ .$

Нам дано расстояние между центрами   $OQ = \sqrt{ 2 ( R^2 + r^2 ) } \ .$

Внешняя касательная   $AS \ .$

Внутренние касательные, пересекающиеся в точке   $D \ ,$
отмечены, как   $CP \$    и   $DL \ .$

Из соображений симметрии, очевидно, что точка   $D \in OQ \ ,$    а сами врутренние касательные отклонены от   $OQ$    на одинаковый угол в разные стороны.

Через точку   $D \$    проведём   $DH \perp OQ \ .$

Обозначим   $\angle PDH = \angle LDH = \angle BOD = \angle CQD = \varphi \ ;$

Отметим точку   $E \$    на продолжении   $QC \ ,$    так, чтобы   $\Delta EQO \$    – был прямоугольным с прямым углом   $\angle E \ .$

Мы пока ещё не доказали, что   $AS || EQ \ ,$     поэтому не можем сказать, что   $OE = R - r \ ,$ хотя это и видно их рисунка.

Но мы можем найти   $OE \$    через Теорему Пифагора:

$OE = \sqrt{ OQ^2 - EQ^2 } = \sqrt{ ( \sqrt{ 2( R^2 + r^2 ) } )^2 - ( R + r )^2 } = \\\\ = \sqrt{ 2 R^2 + 2 r^2 - R^2 - 2Rr - r^2 } = \sqrt{ R^2 + r^2 - 2Rr } = \sqrt{ ( R - r )^2 } \ ;$

$OE = R - r \ ;$

$\sin{ \varphi } = \sin{ EQO } = \frac{OE}{OQ} = \frac{R-r}{OQ} \ ;$

С другой стороны, в прямоугольной трапеции   $QOTS \ :$
$\cos{SQO} = \frac{R-r}{OQ} = \sin{ \varphi } \ .$

Значит   $\angle SAQ = \varphi \ .$

Т.е.   $\angle PDH = \angle SAQ \ ,$    а поскольку   $DH \perp OQ \ ,$    то и   $AS \perp CP \ ,$    а значит внешняя касательная и одна из внутренних – перпендикулярны.

Вторая внутренняя касательная   $DL \$    отклонена от внешней касательной   $AS \$    на угол   $\angle DVT \ .$

$\sin{ \angle DVT } = \cos{ \angle LDP } = \cos{ ( 2 \angle HDP ) } = \cos{ 2 \varphi } = \\\\ = 1 - 2 \sin^2{ \varphi } = 1 - 2 ( \frac{R-r}{OQ} )^2 = 1 - \frac{ 2( R - r )^2 }{ 2( R^2 + r^2 ) } = \\\\ = 1 - \frac{ ( R - r )^2 }{ R^2 + r^2 } = \frac{ R^2 + r^2 - R^2 + 2Rr - r^2 }{ R^2 + r^2 } = \frac{2Rr}{ R^2 + r^2 } \ ;$

В частности, если радиусы равны,   $\sin{ \angle DVT } = 1 \ ,$    что очевидно верно.

О т в е т : $\varphi \in \{ \ arcsin{ \frac{2Rr}{ R^2 + r^2 } } \ , \ 90^o \ \} \ .$