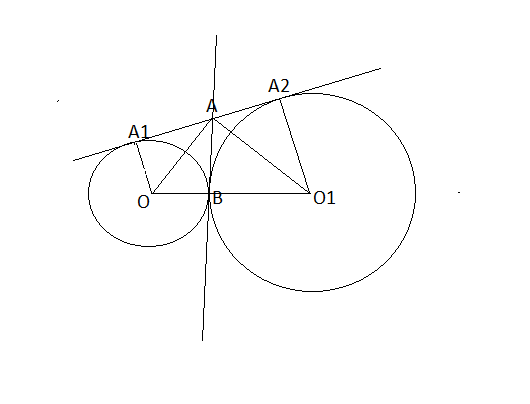\\ график во вложениях \\
Первая окружность с центром в O имеет радиус r = 18. По условию AB = 30 (см. рис.1).
OA делит угол A1AB пополам, O1A делит угол BAA2 пополам. A1AB и BAA2 образуют прямую. Значит угол OAO1 = 90 градусов.
Угол OAB = 90, угол O1BA = 90. AB, таким образом является высотой прямоугольного треугольника OAO1 и делит его на два подобных: OAB и BAO1.
AB/OB = BO1/AB (т.к. треугольники подобны)
BO1 = AB^2/OB
BO1 = 900/18 = 50