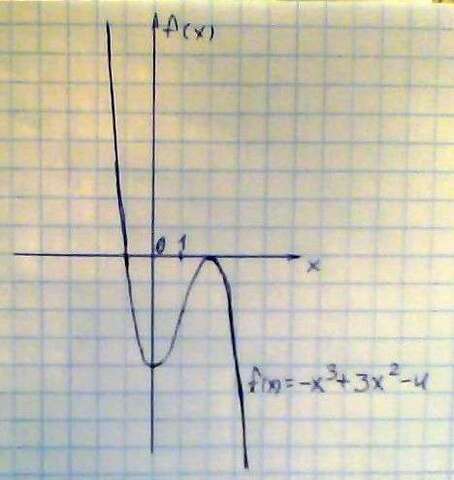
F(x)=-x³+3x²-4.
1. Область определения функции: x∈R (функция определена на x∈(-∞;+∞).
2. Четность/нечетность: f(-x)=-(-x)³+3(-x)²-4=x³+3x²-4≠f(x)≠-f(x) - функция ни четная, ни нечетная.
3. Непрерывность: функция непрерывна на всей области определения.
4. Поведение функции при x→+-∞: при x→-∞, f(x)→+∞; при x→+∞, f(x)→-∞.
5. Производная функции: f'(x)=(-x³+3x²-4)'=-(x³)'+3*(x²)'-4'=-3x²+3*2x-0=-3x²+6x.
6. Экстремумы функции: f'(x)=0, -3x²+6x=0 ⇒ x²-2x=0 ⇒ x(x-2)=0 ⇒ x=0 и x=2.
7. Монотонность (промежутки возрастания и убывания) функции: при x∈(-∞;0], f'(x)<0 - функция убывает, при x∈[0;2], f'(x)>0 - функция возрастает, при x∈[2;+∞), f'(x)<0 - функция убывает. Следовательно x=0 - точка минимума, x=2 - точка максимума.<br>8. Пересечение графика функции с осями координат: с осью абсцисс, f(x)=0 ⇒ -x³+3x²-4=0 ⇒ x=-1 и x=2, получим точки (-1;0) и (2;0); с осью ординат, x=0, f(x)=-4, получим точку (0;-4).
9. Строим график (см. в приложении)