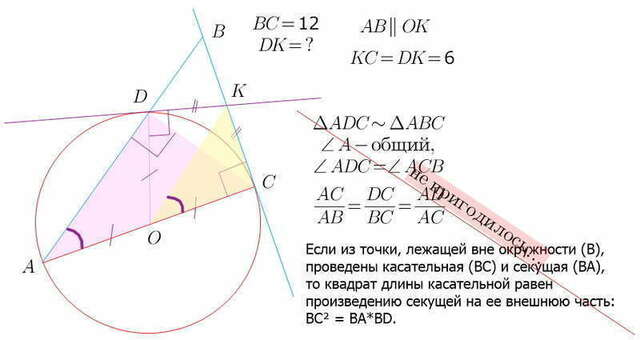
Я формулировку теоремы не стала удалять (повторить всегда полезно))
но она и не пригодилась...
1/ отрезки касательных, проведенных из одной точки (К) равны...
DK=KC
2/ центр вписанной в угол окружности лежит на биссектрисе этого угла))
ОК - биссектриса ∠DKC
∠DKO = ∠CKO
∠DOK = ∠COK
3/ вписанный угол равен половине градусной меры центрального, опирающегося на ту же дугу
∠DAC (опирается на дугу DC) = (1/2)∠DOC = ∠KOC
т.е. DA || KO
О --середина АС ---> KO --средняя линия, К --середина ВС
DK = KC = (1/2)BC = 6