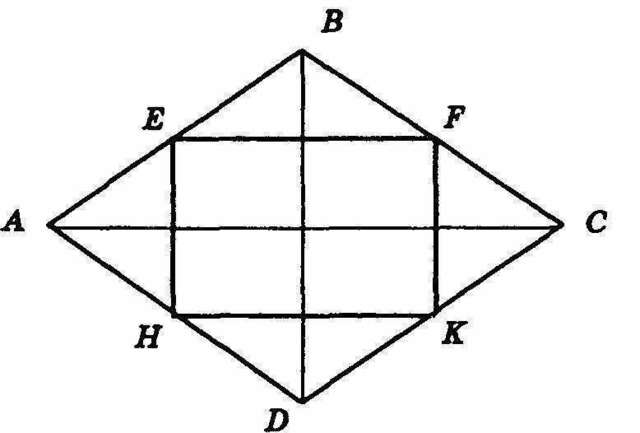
Дано:
ABCD-ромб
AE=EB=BF=FC=CK=KD=DH=HA
----------------------------------------------
Доказать: EFKH-прямоугольник
Доказательство:
Т.к. EF, FK, KH, HE - средние линии треугольников DAB, ABC, BCD и CDA соответственно, то HE II DB, EF II AC, FK II BD, KH II CA. По свойству ромба его диагонали перпендикулярны, значит все углы EFKH - прямые, следовательно, EFKH - прямоугольник (по определению), ч.т.д.