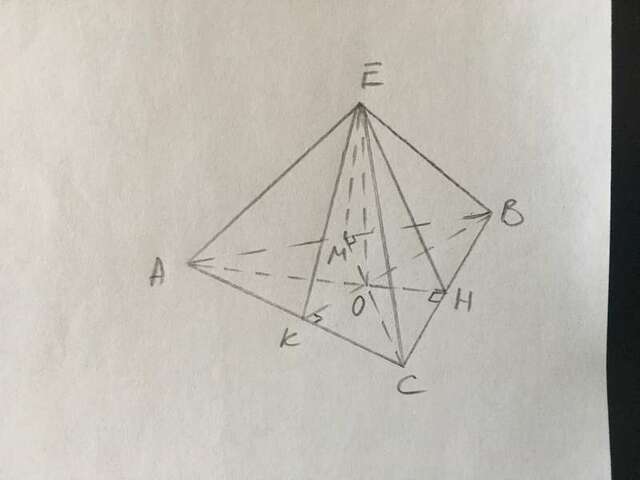
АВСЕ - пирамида с вершиной Е.
В основании лежит правильный тр-ник, для которого радиус описанной окружности в два раза больше радиуса описанной окружности. r=R/2.
ОК=ОВ/2=2а/2=а.
ЕК - апофема на сторону АС.
В тр-ке ЕКО ЕК²=ЕО²+ОК²=3а²+а²=4а²,
ЕК=2а - апофема.
б) ЕК/ОК=2а/а=2. В прямоугольном треугольнике ЕОК гипотенуза ЕК вдвое больше катета ОК, значит ∠КЕО=30°, следовательно ∠ЕКО=60° - угол между боковой гранью и основанием.
в) Площадь боковой поверхности: Sб=Р·l/2, где Р - периметр основания, l - апофема.
R=AB/√3 ⇒ AB=R√3=2a√3.
P=3AB=6a√3.
Sб=6a√3·2a/2=6a²√3 (ед²).