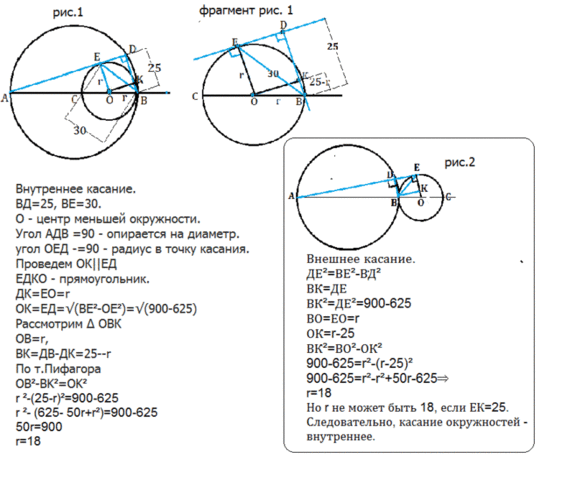
Первая окружность построена на AB, как на диаметре, а вторая — на BC. Прямая, проходящая через точку A, повторно пересекает первую окружность в точке D и касается второй окружности в точке E, BD=25, BE=30. Найдите радиус меньшей из окружностей, если точки A, B и C лежат на одной прямой ------------
В условии не указано, каким образом окружности касаются - внутренним или внешним способом.
Внутреннее касание.
ВD=25, ВЕ=30.
О - центр меньшей окружности.
Угол АDВ =90º - опирается на диаметр.
угол ОЕD -=90º - радиус в точку касания.
Проведем ОК||ЕD
ЕDКО - прямоугольник.
DК=ЕО=
r
ОК=ЕD=√(BE²-OE²)=√(900-625)
Рассмотрим ∆ ОВК ОВ=r,
ВК=DВ-DК=25-r
По т.Пифагора
OB²-BK²=OK²
r ²-(25-r)²=900-625
r² - (625- 50r+r²)=900-625
50r=900
r=18
------
Внешнее касание.
ДЕ²=ВЕ²-ВД²
ВК=ДЕ
ВК²=ДЕ²=900-625
ВО=ЕО=r
ОК=r-25
ВК²=ВО²-ОК²
900-625=r²-(r-25)²
900-625=r²-r²+50r-625⇒
r =18
Но
r не может быть 18, если ЕК=25.
Вывод: касание окружностей - внутреннее.
Возможно, именно для выяснения способа касания условие дано в таком странном виде, если это не ошибка автора вопроса.
В приложении даны рисунки к обоим способам касания.