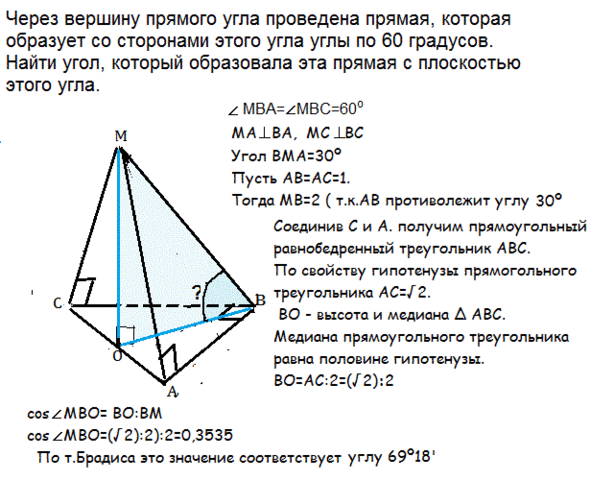
Приложенный к решению рисунок для наглядности дан в несколько ином, чем в условии, ракурсе.
Итак, из вершины прямого угла провели наклонную, образующую с его сторонами углы, равные 60º Нужно найти угол наклона этой прямой к плоскости угла. Обозначим вершину угла В, На его сторонах отложим равные отрезки ВС и ВА. и проведем из А и С перпендикуляры к сторонам угла до пересечения с наклонной в точке М
Угол ВМА=30º
Пусть АВ=АС=1.
Тогда МВ=2 ( т.к.АВ противолежит углу 30º
Соединив С и А. получим прямоугольный равнобедренный треугольник АВС. По свойству гипотенузы такого треугольника
АC=√2.
Проведем ВО - высоту и медиану ∆ АВС.
Медиана прямоугольного треугольника равна половине гипотенузы.
ВО=АС:2=(√2):2
cos MBO= BO:BM
cos MBO=(√2):2):2=0,3535
По т.Брадиса это значение соответствует углу 69º18'