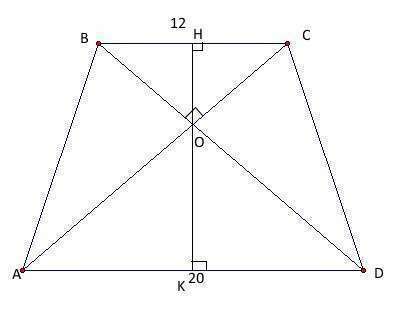
1. Найдите площадь равнобедренной трапеции, диагонали которой перпендикулярны, а основания = 12 и 20 см.
Решение:
В прямоугольном треугольнике медиана,проведенная к гипотенузе, равна половине гипотенузы. Поэтому HO = BC/2 = 12/2 = 6, а OK = AD/2 = 20/2 = 10. Высота трапеции равна HO + OK = 16.
Площадь трапеции:
(12+20)/2 * 16 = 256
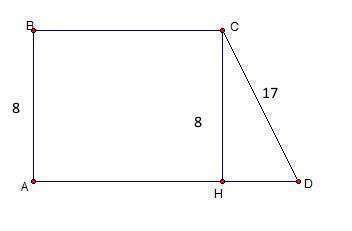
2. Боковые стороны прямоугольной трапеции = 17 и 8 см, а основания относятся как 2:5. Найти площадь.
Решение:
Найдем HD по т. Пифагора:
HD² = CD²-CH² = 17² - 8² = 289 - 64 = 225
HD = 15
Справедливо:

2*(BC +15) = 5BC
3BC = 30
BC = 10.
Тогда AD = AH + HD = BC + HD = 10 + 15 = 25.
Площадь трапеции:
S = (BC+AD)/2 * CH = (10 + 25)/2 * 8 = 35 * 4 = 140