Чтобы выпилить из круглого бревна наиболее прочную балку с поперечным сечением в форме...

Question

Чтобы выпилить из круглого бревна наиболее прочную балку с поперечным сечением в форме прямоугольника на практике поступают так: проводят диаметр АС круга, делят его на три равные части, через точки деления Т и К проводят перпендикуляры к диаметру до пересечения с окружностью в точках В и D. Вычислите меньшую сторону прямоугольника АВСD в сечении такой балки, выпиленной из бревна диаметром 30 см. Ответ округлите до целого числа сантиметров.

Answer 1

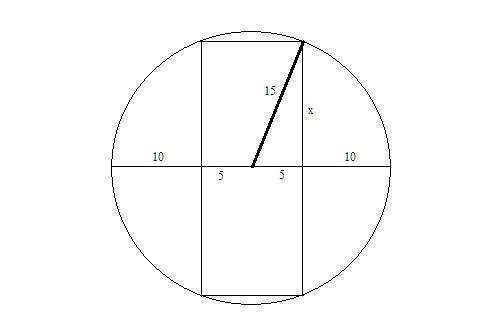
Диаметр бревна 30, значит, радиус 15 см. На рисунке все видно.
Более короткая сторона равна как раз 30/3 = 10 см.
А более длинная равна 2x, где
x^2 = 15^2 - 5^2 = 225 - 25 = 200
x = 10√2 ~ 14,14 см
Значит, более длинная сторона бруса равна примерно 28 см.

---