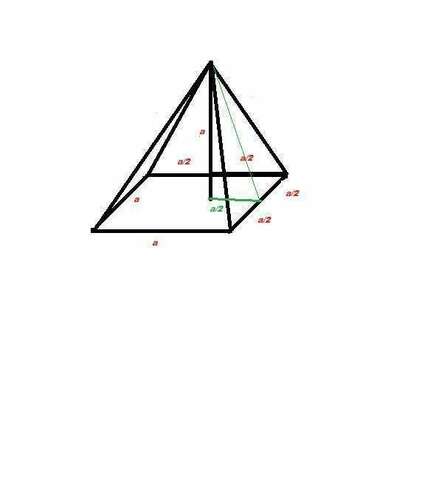кто решит все задачи вместе с решением дам 48 пунктов

1) 180-40=140 - сума двух противоположных углов; 140/2=70 один угол. Ответ: 4) 70⁰

2) допусти, что боковая сторона равна 1, тогда сонование равно √(1*1+1*1)=√2 и получается что стороны относятся как 1 к √2, но призма трёхугольная и получится что их площади относятся как 1 к 3√2. Ответ: 4) 3√2

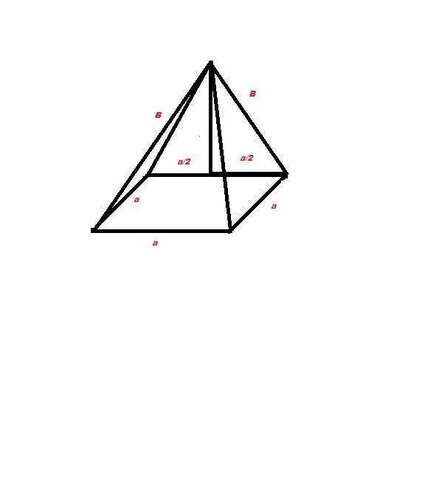
3) так как площадь основания пирамиды равна, $S=\frac{\sqrt{3}}{4}a^2$ , если пирамиду пересекает по середине, получается что отношение сторон будет 2 к 1, получим:

$S=\frac{\sqrt{3}}{4}(\frac{a}{2})^2=\frac{\sqrt{3}}{4*4}a^2=\frac{\sqrt{3}}{16}a^2$ Ответ: 2) $\frac{a^2\sqrt{3}}{16}$

4) треугольник равнобедреный с основанием α, имеем формулу: α=2β*sin(120/2)=β*√3; β=α/(√3)

По формуле площади равнобедреного треугольника получим: $S=\frac{a}{4}\sqrt{\frac{4}{3}a^2-a^2}=\frac{a^2}{4\sqrt{3}}$

5) высота на боковой стороне пирамиды равна: $x=\sqrt{a^2+\frac{a^2}{4}}=\frac{a}{2}\sqrt{5}$

угол между боковой стороной и онованием равен: $sin\alpha=\frac{a}{\frac{a\sqrt{5}}{2}}=\frac{2}{\sqrt{5}}$

Угол между боковыми гранями равен 90, так как пирамида с 4-х угольныи основанием.