Решите пожалуйста В квадрате со стороной 5 см расположено 26 точек. Докажите, что среди...

Дан 1 ответ

Правильный ответ

Разобьём квадрат со стороной 5 см на 25 квадратов со стороной 1 см. Будем рассматривать их как контейнеры. Точка попадает в контейнер, если она лежит либо на его сторонах, либо во внутренней области. Тогда, по принципу Дирихле, хотя бы в одном из контейнеров окажется две точки. [Некоторые точки могут попасть сразу в четыре контейнера (если такая точка упадёт на вершину квадрата, которая не лежит на стороне исходного квадрата), но для нас важно, что любая точка с необходимостью попадает хотя бы в один.]
Итак, в одном из контейнеров содержится две точки. Вспомним, что наш контейнер не что иное, как квадрат со стороной в 1 см.
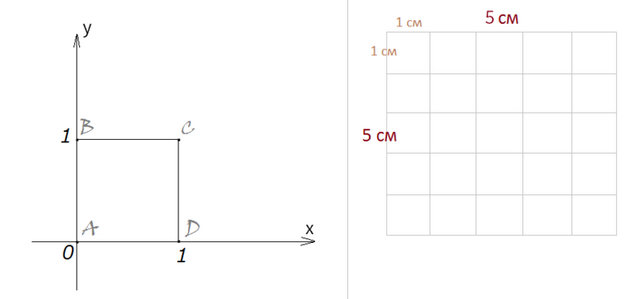
Покажем, что расстояние между двумя точками квадрата со стороной в 1 см не превышает √2. Рассмотрим квадрат ABCD (рис.1) со стороной равной 1 см и две произвольные точки, которые лежат на квадрате.

$\displaystyle z_1 = (x_1, \ y_1), \ z_2 = (x_2, \ y_2)\\\\ d(z_1, z_2) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}\\\\ 0 \leq x_1 \leq 1, \ 0 \leq x_2 \leq 1, \ 0 \leq y_1 \leq 1, \ 0 \leq y_2 \leq 1\\\\ - 1 \leq x_1 - x_2 \leq 1, \ - 1 \leq y_1 - y_2 \leq 1\\\\ 0 \leq (x_1 - x_2)^2 \leq 1, \ 0 \leq (y_1 - y_2)^2 \leq 1\\\\ 0 \leq (x_1 - x_2)^2 + (y_1 - y_2)^2 \leq 1 + 1 = 2\\\\ 0 \leq \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} \leq \sqrt{2}$

Что и требовалось доказать.

Voxman_zn (8.8k баллов) 18 Апр, 18