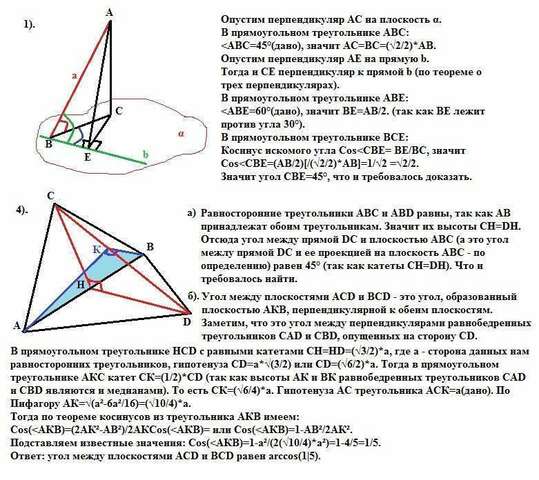
1) Опустим перпендикуляр АС на плоскость α.
В прямоугольном треугольнике АВС: Опустим перпендикуляр АЕ на прямую b.
Тогда и СЕ перпендикуляр к прямой b (по теореме о трех перпендикулярах).
В прямоугольном треугольнике АВE:
В прямоугольном треугольнике ВСE:
Косинус искомого угла Сos<СBE= ВЕ/ВС, значит <br>Сos<СBE=(АВ/2)[/(√2/2)*АВ]=1/√2 =√2/2.<br>Значит угол СВЕ=45°, что и требовалось доказать.
4 а) Равносторонние треугольники АВС и АВD равны, так как АВ принадлежат обоим треугольникам. Значит их высоты СН=DН. Отсюда угол между прямой DC и плоскостью АВС (а это угол между прямой DC и ее проекцией на плоскость АВС - по определению) равен 45° (так как катеты СН=DH). Что и требовалось найти.
4б) Угол между плоскостями ACD и ВСD - это угол, образованный плоскостью АКВ, перпендикулярной к обеим плоскостям. Заметим, что это угол между перпендикулярами АК и ВК равнобедренных треугольников САD и СВD, опущенных на сторону СD.
В прямоугольном треугольнике НСD с равными катетами СН=НD=(√3/2)*а, где а - сторона данных нам равносторонних треугольников, гипотенуза СD=а*√(3/2) или CD=(√6/2)*а. Тогда в прямоугольном треугольнике АКС катет СК=(1/2)*СD (так как высоты АК и ВК равнобедренных треугольников СAD и СВD являются и медианами). То есть СК=(√6/4)*а. Гипотенуза АС треугольника АСК=а(дано). По Пифагору АК=√(а²-6а²/16)=(√10/4)*а.
Тогда по теореме косинусов из треугольника АКВ имеем:
Cos(<АКВ)=(2АК²-АВ²)/2АКCos(<АКВ)= или Cos(<АКВ)=1-АВ²/2АК².<br>Подставляем известные значения:
Cos(<АКВ)=1-а²/(2(√10/4)*а²)=1-4/5=1/5.<br>Ответ: угол между плоскостями АСD и ВСD равен arccos(1|5).