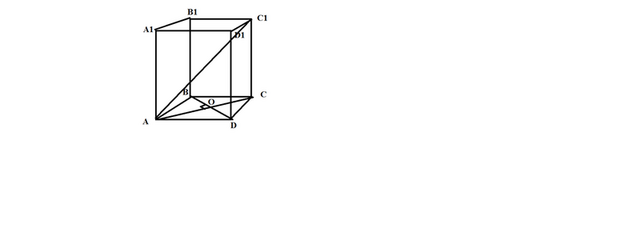
Объем прямой призмы равен произведению основания на высоту призмы.
V=Sh
Sромба=¹/₂d₁*d₂ (1/2 произведения диагоналей ромба)
Диагонали ромба пересекаются под углом 90°.
В Δ САС₁ ∠С₁СА=90°
АС₁ =12см- диагональ призмы,угол наклона к основанию ∠С₁АС=45°⇒∠С₁АС=∠АС₁С=45°
Найдем диагональ ромба по теореме Пифагора:
АС₁²=АС²+СС₁²
Пусть АС²=СС₁²=х² ⇒
2х²=12²
2х²=144
х²=72=√36*2=6√2⇒ высота призмы СС₁=6√2
Найдем меньшую диагональ ромба
См. Δ DАВ^
АD=АВ, ∠DАВ=60°⇒∠АDВ=∠АВD=60°
ΔАВD - равносторонний
АО - высота, биссектриса и медиана ⇒
∠ОАВ=60:2=30°, ∠АОВ=90°, АО=(6√2)/2=3√2
ОВ/АО=tq 30°=√3/3
ОВ=АО*tq 30°=3√2*√3/3=√2*√3=√6
DВ=2ОВ=2√6
S ромба АВСD=¹/₂АС*ВD=2√6*6√2=24√3(см²)
V=Sh
V=24√3*6√2=144√6(cм³)