Всегда верно, что X\Y = X∩{–Y}, где {–Y} – обратное к Y множество.
Всегда верно, что [ X∩Y ] ∪ [ X∩Z ] = X∩(Y∪Z) ;
Всегда верно, что Y∪Z = –( [–Y] ∩ [–Z] ) ;
Всегда верно, что X∩(–X) = { 0 }, где { 0 } – ноль-множество.
Тогда:
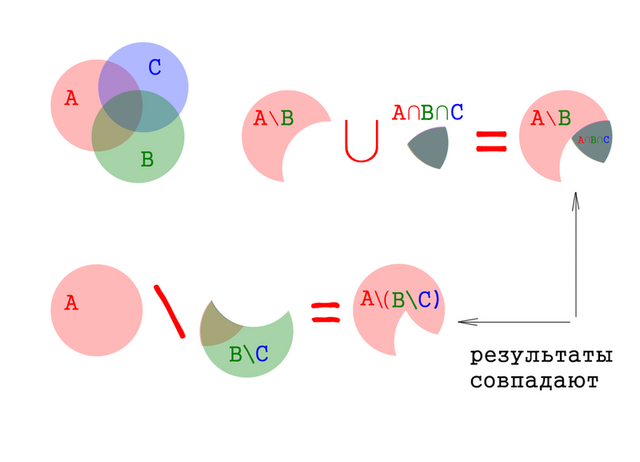
(A\B)∪(A∩B∩C) = ( A ∩ [–B] ) ∪ ( A ∩ [B∩C] ) = A ∩ ( [–B] ∪ [B∩C] ) =
= A \ { – ( [–B] ∪ [B∩C] ) } = A\( B ∩ [ – {B∩C} ] ) = A\( B \ [ B∩C ] ) = A\(B\C) ;
Что и требовалось.
О т в е т : (A\B)∪(A∩B∩C) = A\(B\C) .