Всегда верно, что X\Y = X∩{–Y}, где {–Y} – обратное к Y множество.
Всегда верно, что { –(Y∩Z) } = (–Y) U ( –Z ) ;
Всегда верно, что X∩(YUZ) = [ X∩Y ] U [ X∩Z ] ;
Всегда верно, что X∩(–X) = { 0 }, где { 0 } – ноль-множество.
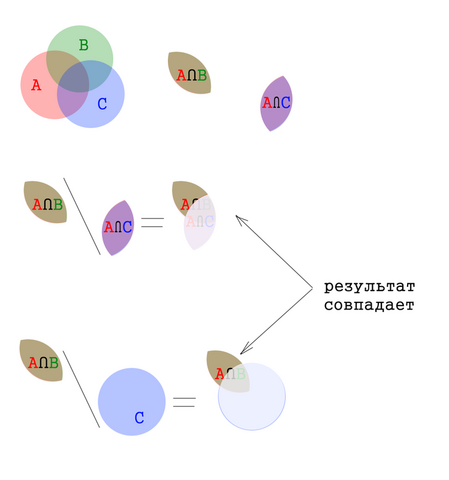
(A∩B)\(A∩C) = ( A∩B ) ∩ { –(A∩C) } = ( A∩B ) ∩ { (–A) U (–C) } =
= [ (A∩B)∩(–A) ] U [ (A∩B)∩(–C) ] = { 0 } U [ (A∩B)∩(–C) ] = (A∩B)\C
Что и требуется доказать.