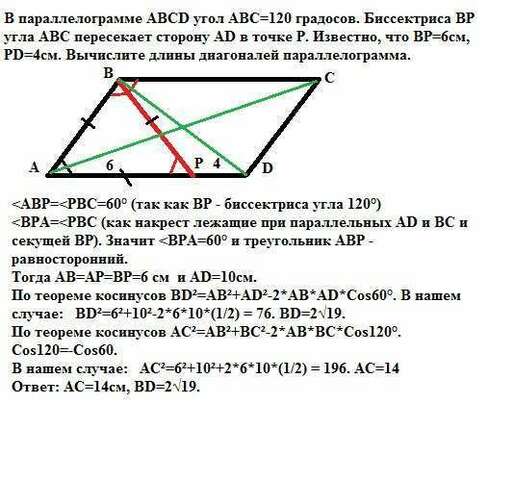
Тогда АВ=АР=ВР=6 см и АD=10см.
По теореме косинусов BD²=AB²+AD²-2*AB*AD*Cos60°. В нашем случае: BD²=6²+10²-2*6*10*(1/2) = 76. BD=2√19.
По теореме косинусов АС²=AB²+ВС²-2*AB*ВС*Cos120°.
Сos120=-Cos60.
В нашем случае: АС²=6²+10²+2*6*10*(1/2) = 196. АС=14
Ответ: АС=14см, ВD=2√19.