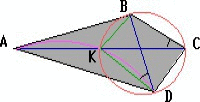
Четырехугольник ABDC. Проводим диагонали и биссектрису DK. Точка К - точка пересечения диагонали AC и DK. ∠ KDB = 55°, т.к. DK - биссек. ⇒ он равен ∠KCB = 35° (по услов) ⇒ Точки K C B D лежат на одной окружности (см. рис.) Получается, вписанный четырехугольник, у которого противоположные углы в сумме 180°. Из этого следует:
∠BKC = ∠BDC = 40°
∠ABK = ∠BKC - ∠ BAC = 40 - 20 = 20°
Тогда BK = AB ⇒ Тогда радиус первой окружности (около AKD) равен радиусу второй (∠ADK = ∠KDB = 55°) Поэтому:
∠CAD = ∠ ACD = 
Следовательно, угол между диагоналями равен:
∠BDC + ∠ACD = 40 + 15 = 55°
Ответ: 55 °