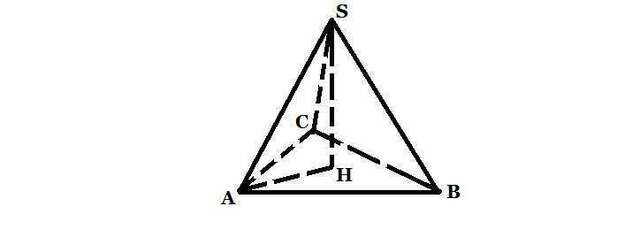
Постоим треугольник ASH (см. приложение). Найдем AH по т. Пифагора: AH = √(144 - 36) = 6√3 дм. Так как треугольник ABC - равносторонний, то точка H - центр описанной окружности, а AH - ее радиус. Найдем длину стороны основания из формулы радиуса описанной около правильного треугольника окружности: R = a÷√3 ⇒ a = R*√3 = 6√3 * √3 = 18 дм. Весь объем пирамиды можно найти по формуле: a²*h÷4√3 = 18²*6÷4√3 = 162√3 дм³.