Диагональ BD четырехугольника ABCD является биссектрисой его угла, BC*BA=BD2 . Докажите,...

Question

Диагональ BD четырехугольника ABCD является биссектрисой его угла, BC*BA=BD2 . Докажите, что LBAD=LBDC. В каком отношении площадь четырехугольника делится его диагональю BD, если известно, что DC:AD=3:2

Answer 1

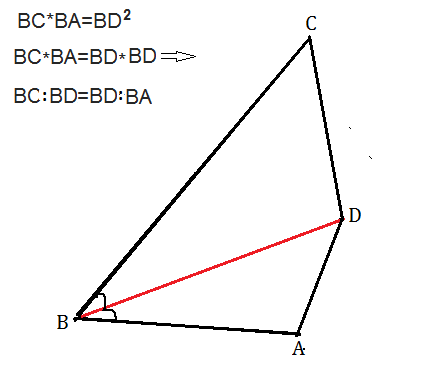
По условию
     ∠СВД, заключенный между СВ и ВД, равен ∠АВД, заключенному между АВ и ВД   
      ВС×ВА=ВД*ВД;  отсюда следует пропорция: 
ВС:ВД=ВД:АВ. 
Если две сто­ро­ны од­но­го тре­уголь­ни­ка про­пор­ци­о­наль­ны со­от­вет­ствен­но двум сто­ро­нам дру­го­го тре­уголь­ни­ка, а углы, за­клю­чён­ные между этими сто­ро­на­ми, равны, то такие тре­уголь­ни­ки по­доб­ны.
      В подобных треугольниках против сходственных сторон лежат равные углы, ⇒  ∠ВАД=∠ВДС  
 Отношение сходственных сторон  DC:AD=3:2,  k=3/2  
  Отношение площадей подобных фигур равно квадрату коэффициента подобия:S ∆   CBD:S ∆ ABD=k²S ∆ CBD:S ∆ ABD=9/4

---