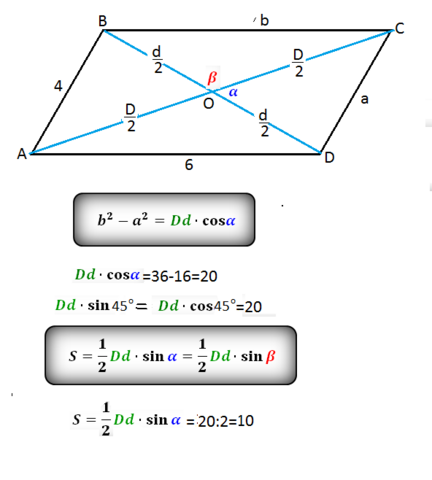
Для параллелограмма есть формула
b²-а²=D*d*cos α
где b и а- большая и меньшая стороны, D и d - большая и меньшая диагонали, α - угол между диагоналями.
Подставим известные величины:
36-16= D*d*cos 45º
D*d*cos45º =20
Одна из формул площади параллелограмма S=Dd* sinα:2
Синус и косинус 45º равны⇒
D*d*sin45º =20
S =Dd* sin45º:2=20:2=10(ед. площади)
---------
Данная выше формула выводится из т.косинусов.
-------
Обозначим для удобства большую сторону ВС параллелограмма b, меньшую СD- а, угол COD-α
Рассмотрим треугольник ВОС
Угол ВОС тупой и его косинус отрицательный.
По т.косинусов из ∆ ВОС
ВС²==ВО²+СО² -2ВО*СО*(-cosα)
b²= (d/2)²+(D/2)² + 2(d/2)*D/2*cos α
Из треугольника СОD по т.косинусов
а²=(d/2)²+(D/2)² - 2(d/2)*D/2*cos α
Вычтем из первого уравнения второе:
b²-а²= (d/2)²+(D/2)² + 2(d/2)*D/2*cos α - (d/2)² - (D/2)² + 2(d/2)*D/2*cos α
b²-а²= 4(d/2)*D/2*cosα=4Dd/4)*cos α
b²-а²=D*d*cos α