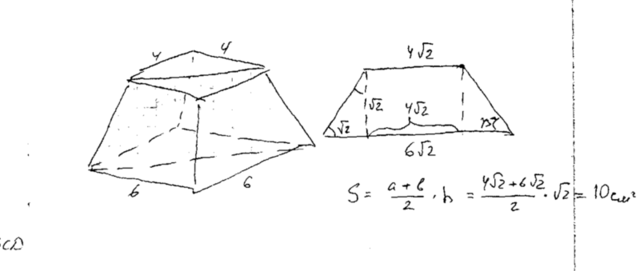
Диагональное сечение правильной усеченной четырехугольной пирамиды является равнобедренной трапецией, основания которой
4√2 и 6√2( их находим по теореме Пифагора), а боковые стороны образуют с основаниями углы по 45°. Начерти эту трапецию и проведи в ней 2 высоты: получится прямоугольник и два прямоугольных равнобедренных треугольника( у них углы по 45°). Горизонтальный катет находим (6√2 - 4√2) / 2 = √2. Такая и высота трапеции. S =(4√2 + 6√2) / 2*√2 = 5√2 * √2 = 10 cм². К доске с этим ответом. "5" обеспечена.