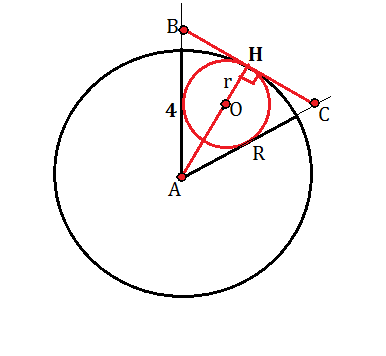
Окружность вписана в сектор, значит, она касается радиусов и дуги, на которую опирается центральный угол.
А - центр большей окружности,
угол А=60º
Н -точке касания вписанной в сектор окружности с дугой.
ВС - касательная к точке H.
∠АНС=∠ВНС=90º
Центр вписанной в угол окружности лежит на его биссектрисе.
АН- биссектриса∠ВАС
∠ВАН=САН=30º
∆ ВАН= ∆ САН
∠АВС=∠АСВ=60º
∆ АВС - равносторонний с высотой АН=R=4 см
Радиус r вписанной в правильный треугольник окружности равен 1/3 её высоты.
r =4/3 см
Ѕ=πr²=(4/3)² π=16/9π см²