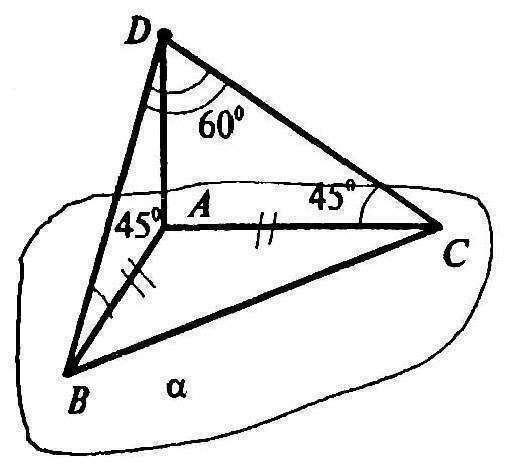
Пусть D - данная точка. DB и DC - наклонные. Проведем AD — перпендикуляр к плоскости α. Тогда АВ и АС — проекции наклонных на плоскость α. Тогда ΔABD и ΔACD — прямоугольные, равнобедренные. Так что АВ = АC = AD = а.
Из этих же треугольников находим:
DC=DB=a:sin45=a√2
Так что ΔBDC — равнобедренный, а поскольку ∠BDC = 60°, то значит треугольник BDC — равносторонний, т.е. DB=DC=BC=a√2