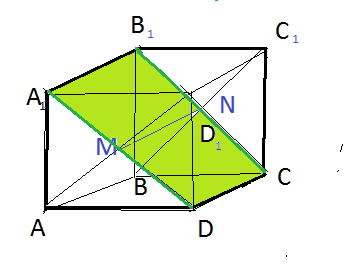
Все грани куба- квадраты.
Диагонали квадрата в точке пересечения взаимно перпендикулярны и делятся пополам.
Проведем в грани В₁ВСС₁ диагонали: ВС₁ и В₁С, они пересекаются в точке N.
ВС₁⊥ В₁С как диагонали квадрата ⇒ BN ⊥ В₁С
Ребро А₁В₁⊥ А₁АDD₁ ⇒ А₁В₁⊥ВС₁⇒ А₁В₁⊥ BN
ВN перпендикулярна двум пересекающимся прямым плоскости
А₁В₁ и В₁С плоскости А₁В₁СD⇒BN⊥пл А₁В₁СD.
По условию
BN=8
Аналогично
AM⊥пл А₁В₁СD, M- точка пересечения диагоналей А₁D и AD₁
C₁N⊥пл А₁В₁СD.
D₁M⊥пл А₁В₁СD.
АМ=МD₁=BN=NC₁=8
Расстояния от вершин А, С₁и D₁ равны 8