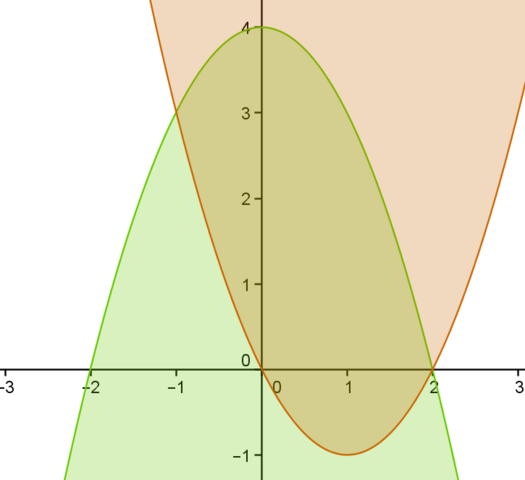
а) Наверно, все-таки y=x^2-2x?
"Поднимем" график на 1 вверх для того, чтобы не задумываться о том, что область делится на 2 части осью Ох. Тогда у нас появятся 2 параболы 5-x^2 и x^2-2x+1. (На самом деле, в интеграле будет фигурировать только разность, и все добавки сократятся)

б)