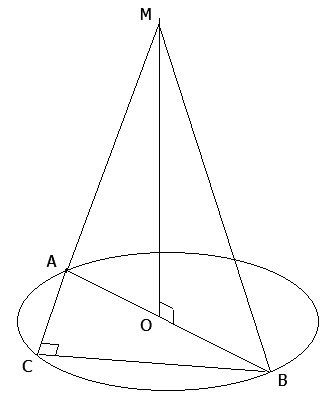
Если все боковые рёбра пирамиды (MA; MB; MC) равны между собой, то вокруг основания пирамиды (ABC) можно описать окружность, причём вершина пирамиды (M) проецируется в её центр (O).
MO ⊥ ABC
Центр окружности (O), описывающей прямоугольный треугольник (ABC), является серединой гипотенузы (AB).
O ∈ AB
МО ∈ MAB
Если плоскость (MAB) проходит через прямую (MO) перпендикулярную другой плоскости (ABC), то эти плоскости перпендикулярны.
MAB ⊥ ABC